Boxplots y Violin Plots, utilidad y visualización con ggplot

analisis
R
Author

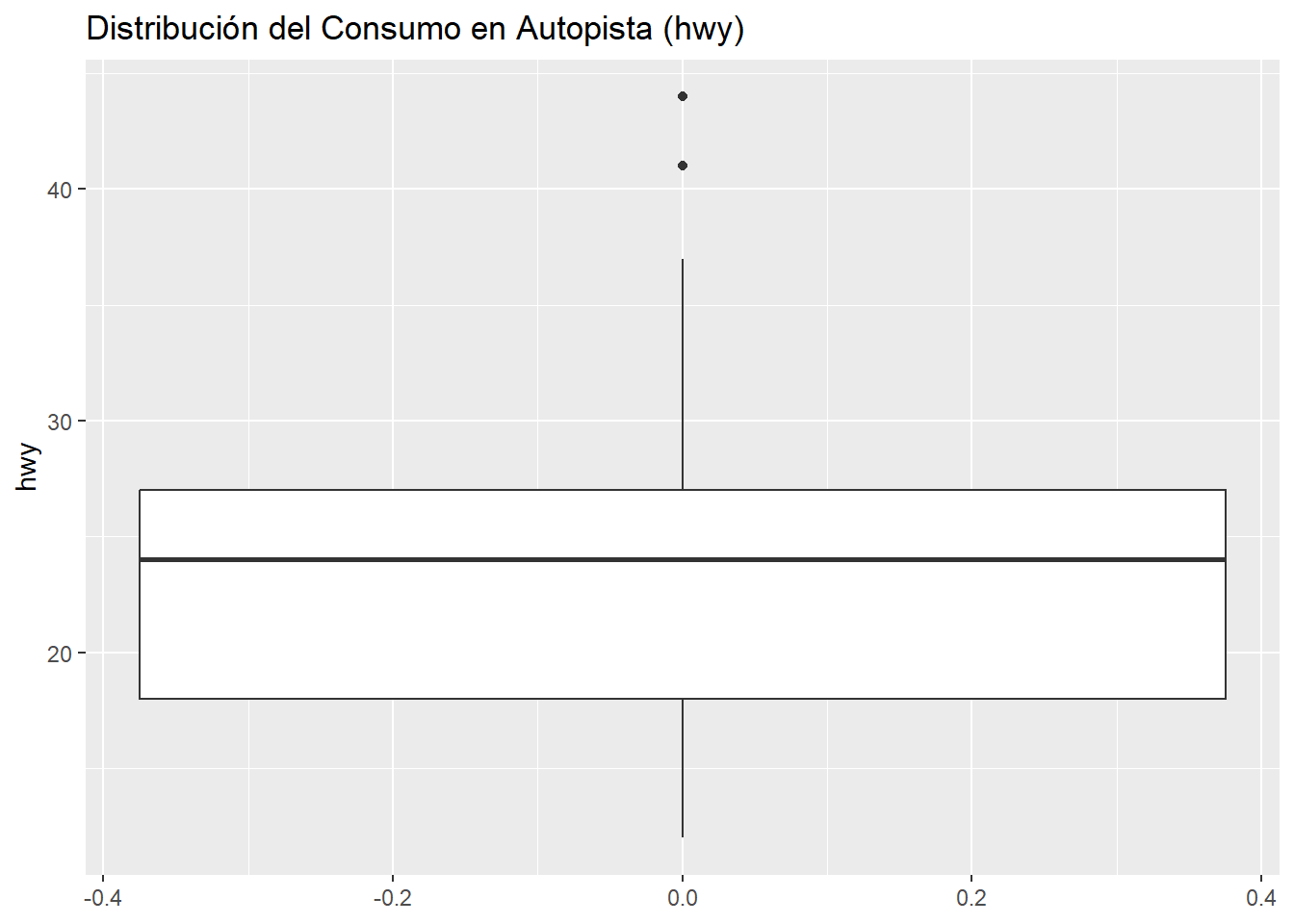
Roberto Gil-Saura

Published

June 27, 2025

Introducción

Cuando analizamos una variable numérica, la media nos da una idea del centro, pero nos deja sin respuesta ante preguntas de análisis: ¿cómo se distribuyen los datos alrededor de ese centro? ¿Están todos los valores agrupados o muy dispersos? ¿Hay valores atípicos extremos? Para responder a estas preguntas, necesitamos ir más allá de los simples promedios.

Aquí es donde entra en juego una de las herramientas más ingeniosas y eficientes de la visualización de datos: el diagrama de caja y bigotes, o boxplot. Creado por el estadístico John Tukey, un boxplot es como una radiografía de tu variable: te permite ver su estructura interna de un solo vistazo.

En este post, nos sumergirnos en el mundo de los boxplots con ggplot2. No solo aprenderás a crearlos con geom_boxplot, sino que también descubriremos a su primo más moderno y revelador, el violin plot (geom_violin). Al final, sabrás exactamente cuándo usar cada uno y cómo combinarlos para el mejor storytelling sobre tus datos.

Parte I: La anatomía de un boxplot (geom_boxplot)

Antes de crear un boxplot, es fundamental entender qué representa cada una de sus partes. Un boxplot resume la distribución de una variable numérica en cinco estadísticas clave, conocidas como el “resumen de cinco números”.

  1. La línea central (Mediana): Es el corazón del gráfico. Representa la mediana (percentil 50), el valor que divide los datos exactamente por la mitad.
  2. La caja (Rango Intercuartílico - IQR): La caja contiene el 50% central de tus datos.
    • El borde inferior de la caja es el primer cuartil (Q1), o percentil 25.
    • El borde superior de la caja es el tercer cuartil (Q3), o percentil 75.
    • La altura de la caja (IQR = Q3 - Q1) es una medida robusta de la dispersión de los datos.
  3. Los bigotes (Whiskers): Se extienden desde la caja para mostrar el rango de la mayoría de los datos. Por defecto, se extienden hasta el valor más lejano que no esté a más de 1.5 veces el IQR de la caja.
  4. Los puntos (Outliers): Cualquier punto de dato que caiga fuera de los bigotes se considera un valor atípico (outlier) y se dibuja individualmente.

Creando nuestro primer boxplot

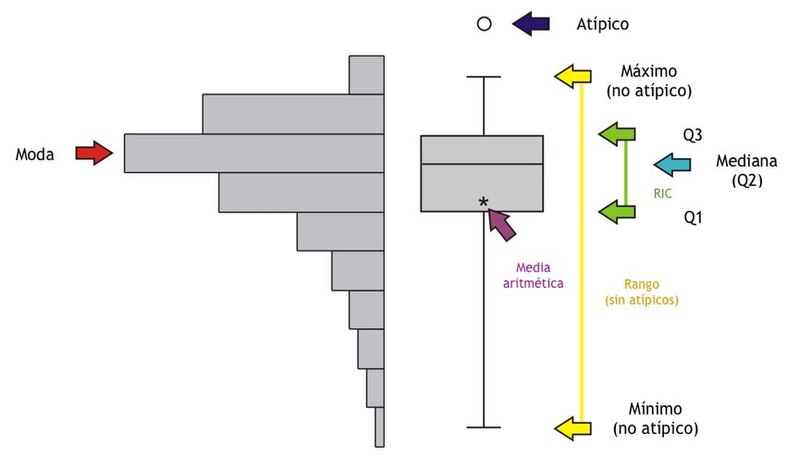
Vamos a usar el dataset mpg para explorar la distribución del consumo en autopista (hwy).

Code 
# Cargar la librería
library(tidyverse)

# Boxplot para una única variable
ggplot(data = mpg, mapping = aes(y = hwy)) +
  geom_boxplot() +
  labs(title = "Distribución del Consumo en Autopista (hwy)")

Comparando grupos

El poder de los boxplots se desata cuando los usamos para comparar la distribución de una variable numérica a través de diferentes grupos categóricos.

Pregunta: ¿Cómo se compara el consumo en autopista (hwy) entre las diferentes clases de coche (class)?

Code 
ggplot(data = mpg, mapping = aes(x = class, y = hwy)) +
  geom_boxplot() +
  coord_flip() + # Giramos el gráfico para que las etiquetas largas se lean mejor
  labs(
    title = "Comparativa de Consumo por Clase de Coche",
    x = "Clase de Coche",
    y = "Consumo en Autopista (Millas por Galón)"
  )

Comparando el consumo en autopista entre diferentes clases de coche.

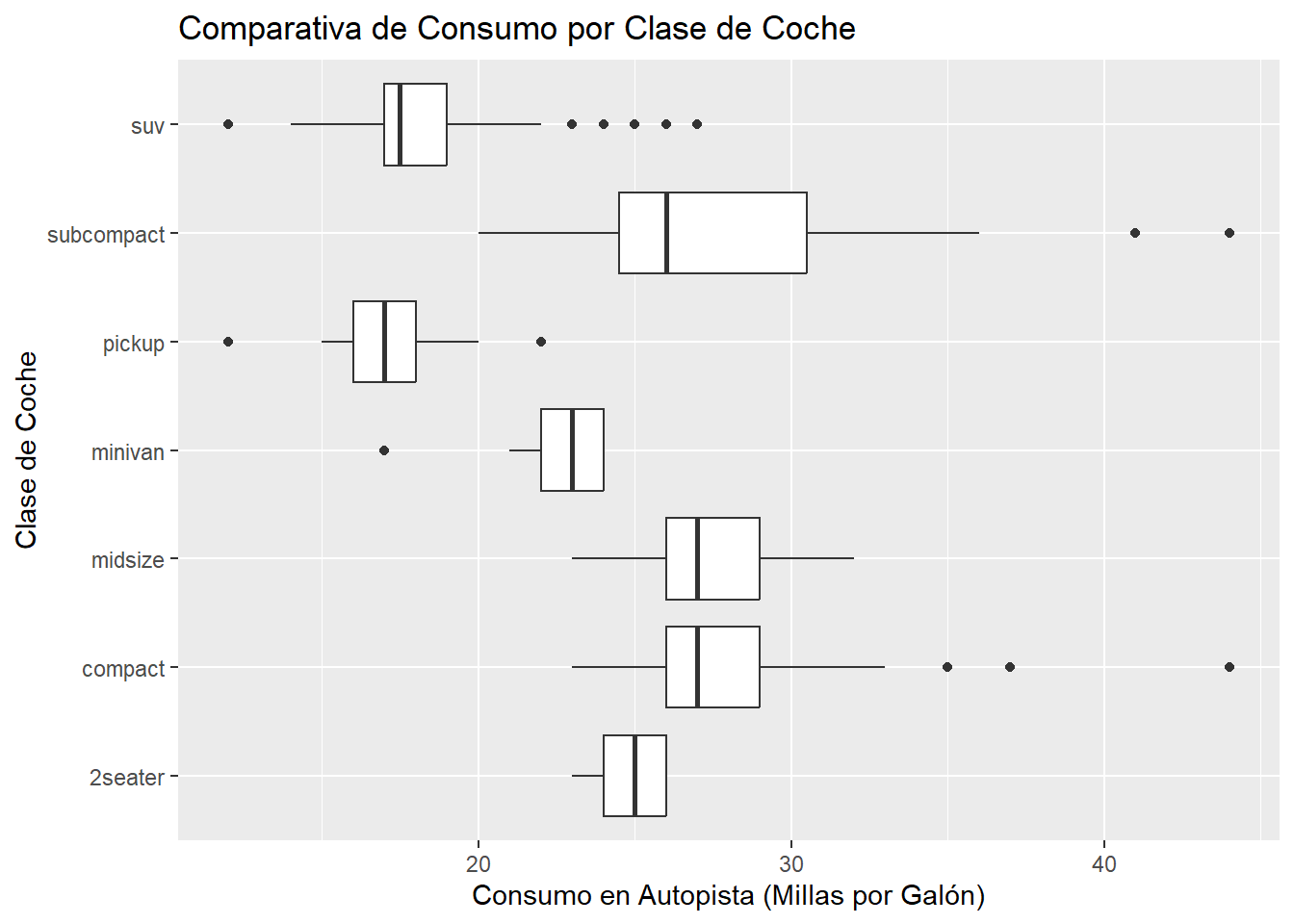
Esta visualización es muy rica. De un vistazo podemos concluir: * Medianas: Los coches compactos (compact) y subcompactos (subcompact) tienen las medianas de consumo más altas (son más eficientes). * Dispersión: La clase suv tiene una dispersión enorme (la caja es muy alta), lo que indica una gran variabilidad en la eficiencia de los SUVs. * Outliers: Hay varios outliers, especialmente un minivan con un consumo inusualmente bajo.

Parte II: El primo moderno - El violin plot (geom_violin)

Un boxplot es una gran vusualización, pero tiene una limitación: oculta la forma de la distribución. No podemos saber si los datos dentro de la caja están distribuidos uniformemente, si tienen un solo pico (unimodal) o varios picos (multimodal).

El violin plot resuelve este problema. Esencialmente, es un boxplot combinado con un gráfico de densidad.

  • ¿Qué es? Un violin plot muestra la misma información de resumen que un boxplot, pero además, su anchura en cada punto representa la densidad de los datos en ese valor.

Vamos a recrear nuestro gráfico anterior usando geom_violin().

Code 
ggplot(data = mpg, mapping = aes(x = class, y = hwy)) +
  geom_violin() +
  coord_flip() +
  labs(
    title = "Comparativa de Consumo por Clase de Coche (Violin Plot)",
    x = "Clase de Coche",
    y = "Consumo en Autopista (Millas por Galón)"
  )

Comparativa usando violin plots.

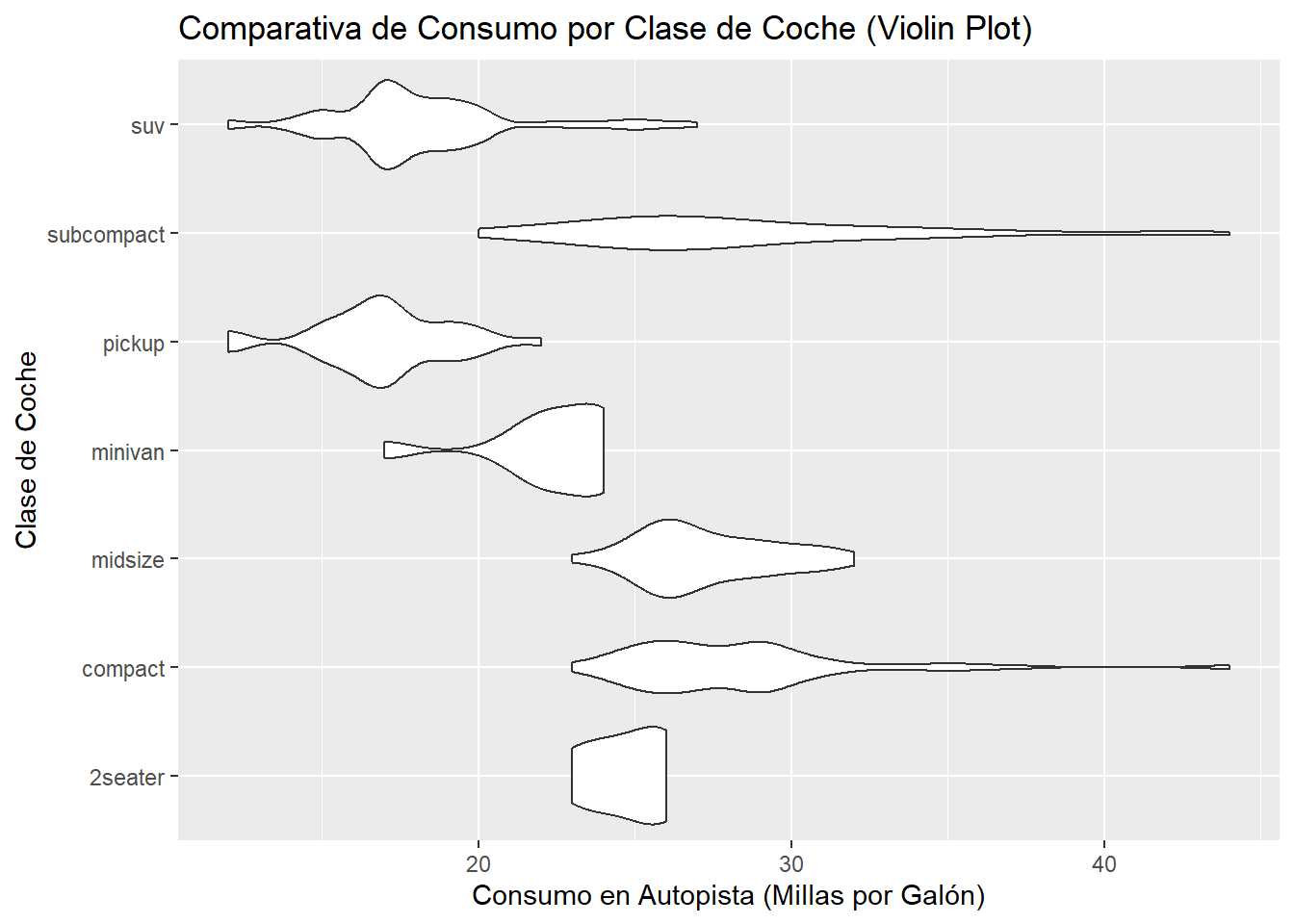
¡La diferencia nos dice cosas de los datos! Vemos cosas que el boxplot oculta:

  • La distribución de los coches compact y midsize no es simétrica; tiene dos picos (es bimodal). Esto podría indicar que hay dos subgrupos de coches dentro de esas clases.
  • La distribución de los suv está claramente sesgada hacia valores más bajos (menos eficientes).

Parte III: Combinando capas

¿Y si no queremos elegir? ¿Y si queremos la robustez estadística del boxplot y la riqueza visual del violin plot? Con ggplot2, podemos tenerlo todo. Simplemente, añadimos ambas geometrías al mismo gráfico.

Code 
ggplot(data = mpg, mapping = aes(x = class, y = hwy, fill = class)) +
  geom_violin(alpha = 0.7, show.legend = FALSE) + # Hacemos el violín semitransparente
  geom_boxplot(width = 0.1, fill = "white", show.legend = FALSE) + # Un boxplot estrecho y blanco en el centro
  labs(
    title = "Visión Completa: Boxplot dentro de un Violin Plot",
    x = "Clase de Coche",
    y = "Consumo en Autopista (Millas por Galón)"
  ) +
  theme_minimal()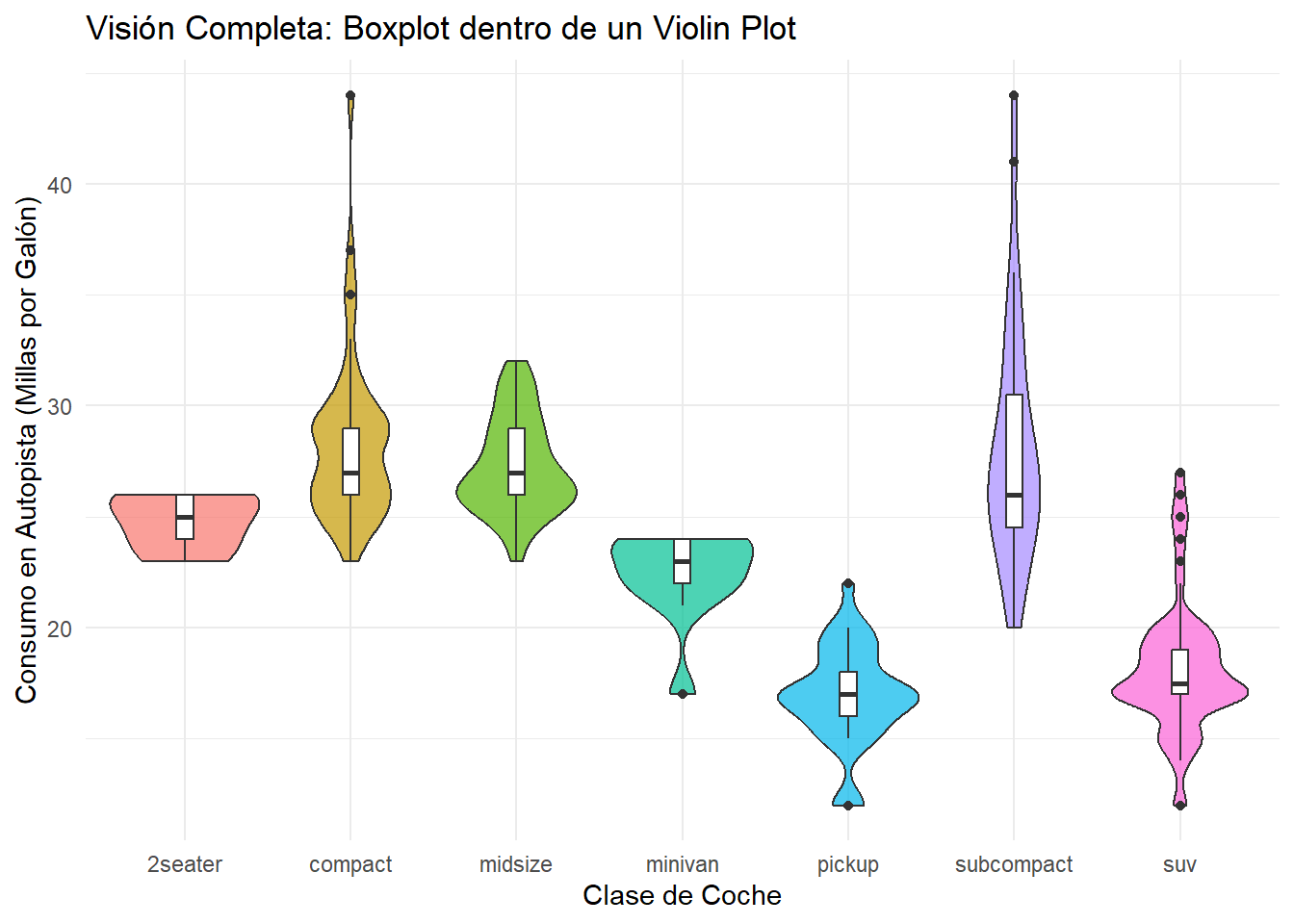

Combinando un violin plot con un boxplot superpuesto.

Esta es, para muchos, la visualización definitiva para comparar distribuciones. Obtenemos: 1. La forma de la distribución gracias al violín. 2. Los estadísticos clave (mediana, cuartiles) de forma precisa gracias al boxplot.

Conclusión: ¿Cuándo usar cada uno?

La elección de la visualización depende siempre de la historia que quieras contar y de tu audiencia.

  • Usa un geom_boxplot cuando:
    • Necesites una comparación rápida y limpia de las medianas y la dispersión.
    • Tengas muchos grupos que comparar (los violines pueden ser visualmente ruidosos).
    • Tu audiencia esté muy familiarizada con los boxplots y quieras ir al grano.
  • Usa un geom_violin cuando:
    • La forma de la distribución sea importante para tu análisis.
    • Sospeches que tus datos pueden ser bimodales o multimodales.
    • Tengas suficientes datos para que la estimación de la densidad sea estable.
  • Usa la combinación de ambos cuando:
    • Quieras la máxima densidad de información en un solo gráfico.
    • Estés realizando un análisis exploratorio profundo o presentando tus hallazgos clave.

Ahora tienes en tu libro de notas dos de las visualizaciones más potentes para ir más allá de las medias y entender verdaderamente la estructura de tus datos.

Referencias

Tukey, J. W. (1977). Exploratory Data Analysis. Addison-Wesley.

Wickham, H. (2016). ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York. https://doi.org/10.1007/978-3-319-24277-4

Healy, K. (2018). Data Visualization: A Practical Introduction. Princeton University Press.